[GIS原理] 10
![[GIS原理] 10](http://oss.aqwf.com/file/p/2024/03-07/1709753358379_0.png)
在知識傳播途中,向涉及到的相關著作權人謹致謝意!
南師國家精品課程《地理信息系統》——主講人:韋玉春老師
文章目錄
【描述性統計】有一個群體,用均值、方差、標準差、眾數,這叫描述性統計
【推斷性統計】有一個大的區域,在這區域里采了幾個樣,對這幾個樣本用描述性統計。然后用這個數據推斷這個區域的數據。推斷性統計基于概率論
【怎么往外推斷呢?】數學分布(正態、二項分布),這個數服從什么分布,在某個概率下,這個分布是成立的–>進行向外推斷
1 空間統計描述 1.1 描述性統計
【描述性統計】
對空間對象分布狀況的統計對具有空間坐標的屬性的統計
【舉例】有多少
長三角地區城市分布具有聚集性?江蘇省人均GDP是多少?
【基本統計量】
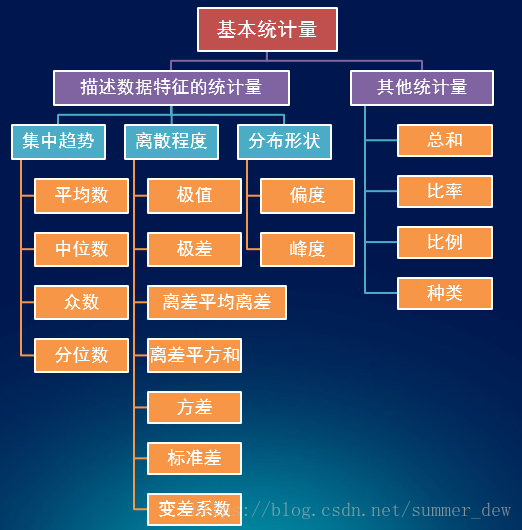
【正態分布】統計學中所有的東西,在大量的情況下,假設的都是正態分布
【規則!】如果你的數據不是正態分布,那么你的數據描述就要用另外一套指標
【舉例】平均成績是80分,你默認的假設是全班成績是服從正態分布的–>如果全部成績放在一起的分布不是正態的,那么這個平均成績就是有偏差的,不合適的
1.2 探索性數據分析
【探索性數據分析】首先是尋找數據的模式和特點,再根據數據特點選擇合適的模型。揭示數據中存在的模式
是空間推斷性統計,探究“怎么分布的?”的問題
【解釋】拿到數據后,要想清楚,你要做什么,你要怎么做,為什么而做?探索性數據分析:天天看數據,找數據的規律,找想法,找個研究方向
【探索性數據分析的重要性】認為,“在認識到你看來多好的測量了它以前,重要的是理解你能做什么”
【動手前的三個問題】
科學問題是怎么產生的:你拿到數據后要干嘛呢?解決的是什么問題?問題不一樣,統計方法不一樣。如何引導產生新的調查設計方案:你這個調查方案是怎么產生的,調查方案怎么選擇如何繼續進行分析:做完之后,將來怎么做呢?
【步驟】數據->數據的數學分布->概率論->推斷
1.2.1 直方圖
【直方圖】
對樣本數據按一定的分級方案(等間隔分級、標準差等)進行分級,統計記錄落入各個級別中的個數或占總樣本數的百分比,然后用條帶圖或柱狀圖表現出來。直方圖可以直觀反映采樣數據分布特征、總體規律,可以用來檢驗數據分布和尋找數據離群值
【特點】
適用于空間對象為點和面的屬性數據簡單易用缺乏空間信息 1.2.2 Q-Q圖
【Q-Q圖】用來輔助判斷樣本數據是否服從正態分布
【做法】做數據的四分位數(四分之一劃分):25%、50%、75%,即是Q-Q圖
【解釋】數據上怎么分布的?Q是的首字母,表示四分位數圖
【拓展】假如數據不是正態分布的
平均數:那么平均數去失去了作用中位數:這時候,中位數就能更好的描述數據四分位數:25%、50%(中位數)、75%

2 空間自相關分析
【空間自相關】空間中相近的樣點具有某種相似性,相距較遠的樣點往往不相似
【作用】解釋和尋找存在的空間聚集性或“焦點”
【舉例】把小偷的點標在地圖上,用空間自相關來分析,找哪里是賊窩
【舉例】葉子的分布:沒有風吹,距離越近,葉子是越厚的。風一吹,越遠葉子越薄
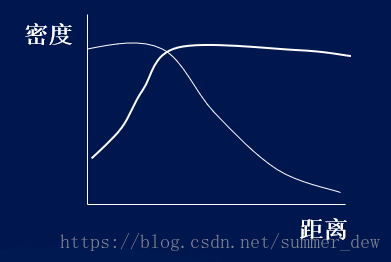
【變異】越近空間越相似–>反過來說:越近空間變異越少,越遠空間的變異越大
2.1 類型 全局(全程)自相關局部自相關:相關的范圍

2.2 自相關的解釋 正自相關:屬性值的差異隨距離變小越相似負自相關:反向相關,屬性值的差異隨距離變小越不相似0:屬性值的差異與距離沒有關系 2.3 自相關性測度
自相關的定量判定,三個統計量
’參數 2.3.1 權重矩陣
【解決的問題】數據的關系,怎么引入到計算里呢?空間權重矩陣(w矩陣)
【空間權重矩陣】是空間自相關分析的基礎
空間數據中隱含的拓撲信息提供了空間鄰近的基本度量,這通常可通過二元對稱的空間權重矩陣W來表達
【怎么做的?】約定:相鄰定義為1,不相鄰定義為0 --> 產生了一個0、1表
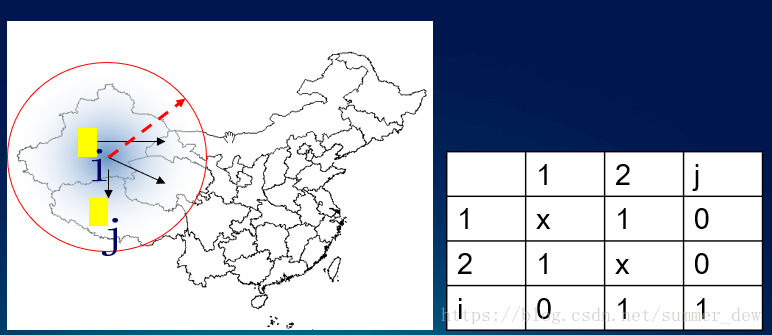
【注意】所有相關的度量都需要經過檢驗,不以值的高低斷英雄,而在置信區間和顯著性(要做一個概率檢驗、顯著性檢驗)
【自相關的取值范圍】[-1,1]
【例子】I=0.001,這個關系是強還是弱呢?不知道,必須做檢驗。根據檢驗之后才知道
【原因】I的大小和樣本數是有關系的
數據量少,只有兩個點的時候,I=0.1那相關性肯定是很弱的數據量有一個億,I=0.1那相關性就已經是很強的了 2.3.2 ’sI
【’sI】包括全程和局部兩個參數,用來分析空間的相關性

【解釋】w=1即是任意一個數對于均值的偏差,和方差的公式很像,只是加了一個w(距離比較近才計算,比較遠w=0就不計算了)
【意義】I值越大,表明正的空間相關性越強
正相關:如果是正的而且顯著,表明具有正的空間相關性。 即在一定范圍內各位置的值是相關的負相關:如果是負值而且顯著的,則具有負的空間相關性,數據之間反相關隨機:接近于0則表明數據的空間分布是隨機的,沒有空間相關性 2.3.3 參數
【應用場景】進行局部自相關分析
【意義】C值大于0,表明正的值四周為高值環繞,小于0,則為低值環繞,0則為無聚集特征。
2.3.4 G統計量
【應用場景】局部自相關分析
【意義】較高的G值表明位置周圍是較高的數據,即數據具有聚集性
【結論】模擬表明 (Ord 和 1994),在xi 周圍不存在空間聚集的原假設的條件下,G的分布接近與正態。對于不同的觀察值N,在不同的顯著性概率下G值各不相同。
【例如】在90%的概率下,N=40對應的G值為2.7913
2.4 應用問題
什么情況下要用空間自相關,用空間自相關用來研究什么問題
【問題】常識是否需要證明?
你已經知道你的研究對象就是聚集的,你還用空間自相關去做,這就沒有必要了
【例子】
螞蟻在空間上是不是空間自相關的?所以不能用空間自相關來研究螞蟻,螞蟻就是一窩一窩的研究蝗蟲在空間上是不是空間自相關?可以的,原先沒有這個概念